Deductive and plausible reasoning

Policeman's conclusion couldn't be a logical deduction
Deductive reasoning consists of the following strong syllogisms:
if $A$ is true, then $B$ is true \begin{align*} \frac{\text{$A$ is true}}{\text{therefore, $B$ is true}} \end{align*}
\begin{align*} \frac{\text{$B$ is false}}{\text{therefore, $A$ is false}} \end{align*}

Weak syllogisms

The reasoning of our policeman consists of the following weak syllogisms:
if $A$ is true, then $B$ is true \begin{align*} \frac{\text{$A$ is false}}{\text{therefore, $B$ becomes less plausible}} \end{align*}
\begin{align*} \frac{\text{$B$ is true}}{\text{therefore, $A$ becomes more plausible}} \end{align*}

Crucial difference

Strong syllogisms can be chained together without any loss of certainty
Weak syllogism have wider applicability

Most of the reasoning people do consists of weak syllogism.

Quantifying weak syllogisms

Question: can we quantify this everyday reasoning?

Answer: yes, using probability theory.

Cox's theorem (1946) states that any system for plausibility reasoning that satisfies certain commonsense requirements is isomorphic to probability theory.

Cox's theorem relies on a few assumptions. Whilst those assumptions are not necessarily how humans always think, it might well something be something that rational people might want to adopt into their way of thinking.

Objectives of this talk

Goal 1: show that probability theory can be regarded as an extension of logic
Goal 2: relate such notion of probability to other approaches of interpreting probability
Goal 3: show applications of probability theory used as logic

Preliminary notation

Proposition: unambiguous statement that is either true or false
Compounded proposition: constructed from other propositions using negation ($\neg$), and ($\wedge$), or ($\vee$), implies ($\implies$), or equivalence ($\iff$)
Atomic proposition: the one that can not be decomposed

Introducing state of knowledge

A state of information $X$ summarises the information we have about some set of atomic propositions $A$, called the basis of $X$, and their relationships to each other. The domain of $X$ is the logical closure of $A$.
Write $(A | X)$ for the plausibility we assign to $A$ given the information in $X$.
$A, X$ is the state of information obtained from $X$ by adding the additional information that $A$ is true.

Assumption: Real-valued

(R1) (A | X) is a single real number. There exists a single real number $T$ such that $(A | X) \leq T$ for every $X$ and $A$.
- Higher numbers should represent higher degree of plausibility. Avoid dealing with $+\infty$ by invoking $f(x) = \arctan(x)$
$X$ is consistent if there's no proposition $A$ such that $(A | X) = T$ and $(\neg A | X) = T$.

Assumption: "Common sense"

(R2) Plausibility assignment are compatible with propositional calculus
1. If $A$ is equivalent to $A'$ then $(A | X)$ = $(A' | X)$
2. if $A$ is a tautology then $(A | X)$ = T
3. $(A | B, C, X) = (A | (B \wedge C), X)$
4. if $X$ is consistent and $(\neg A | X) < T$, then A, X is also consistent

Assumption: Certainty of a belief is singled valued

(R3) There exists a non increasing function $S_0$ such that $(\neg A | X) = S_0 ( A | X)$ for all $A$ and consistent X.
- If $(A | X)$ and $(\neg A | X)$ vary independently from each other then we have a two-dimensional theory as we need 2 numbers to characterise our uncertainty about $(A | X)$
Proposition: $F := S_0(T)$. Then $F \leq (A | X) \leq T$ for all $A$ and consistent X.

Assumption: Universality

(R4) (Universality) There exists a nonempty set of real numbers $P_0$ with the following two properties
- $P_0$ is a dense subset of $(F, T)$
- For every $y_1, y_2, y_3 \in P_0$ there exists some consistent $X$ with a basis of at least three atomic propositions $(A_1, A_2, A_3)$, such that $(A_1 | X) = y_1$, $(A_2 | A_1, X) = y_2$ and $(A_3 | A_1, A_2, X) = y_3$.

Last assumption: Conjunction

(R5) (Conjunction) There exists a continuous function $F:[F, T]^2 \to [F, T]$, such that $(A \wedge B | X) = F((A | B, X), (B | X))$ for any $A, B$ and consistent $X$.
- definition of $F$ could be narrowed down to just 4 possibilites consistently with previous axioms.
Heuristic: for $A \wedge B$ to be true $B$ has to be true so $(B | X)$ is needed. If $B$ is false then $A \wedge B$ is false independently of $A$, so $(A | X)$ is not needed if $(A | B, X)$ and $(B | X)$ are known.

Cox's theorem

There exists a continuous, strictly increasing function $p$ such that, for every $A, B$ consistent with $X$,

$p(A | X) = 0$ iff $A$ is known to be false given the information in $X$.
$p(A | X) = 1$ iff $A$ is known to be true given the information in $X$.
$0 \leq p(A | X) \leq 1$.
$p(A\wedge B | X) = p(A | X)p(B | A, X)$.
$p(\neg A | X) = 1 - p(A | X)$ if $X$ is consistent.

What about Kolmogorov's axioms?

Kolmogorov's probability is defined on a sample space $\Omega$ with an event space $F$ which forms a $\sigma$-algebra

$P(E) \in \mathbb{R}, P(E) \geq 0 \quad \forall E \in F$
$P(\Omega) = 1$
$P \left( \bigcup_{i = 1}^{\infty} E_i \right) = \sum_{i = 1}^{\infty} P(E_i)$ for any countable sequence of disjoint events sets.

Example: Coin toss. Then $\Omega = \{H, T\}$, $F = \{ \emptyset, \{H\}, \{T\}, \{H, T\} \}$. Sample measure $P$ is then just $P(\{H\}) = P(\{T\}) = 1/2$, $P(\emptyset) = 0$, $P(\{H, T\}) = 1$.

Comparisons of Cox's approach with Kolmogorov's

Closure of propositions under (AND, NOT) is remarkably similar to the definition of $\sigma$-algebra. However, care must be taken with regards to countable AND application: but could be dealt with taking a well-behaved limit.

Not all statements could be meaningfully decomposed into a sum of disjoint primitive events, for example "it will rain tomorrow".

The principles for assigning probabilities by logical analysis of incomplete information is not present at all in Kolmogorov system.

Frequencies? Go via MaxEnt route

To relate frequencies with plausibilities we will use MaxEnt principle
Imagine rolling a die some large number of times and observing that the average of all rolls is $4$. What is the probability distribution one should assign to such a die?
$1/6$ to each outcome is ruled out as the average would be $3.5$.

Solution: out of all probability distributions that average to $4$ pick the one which maximise the information entropy: $\sum_{j = 1}^{6} -p_j \log p_j$.
- The answer is: $0.11, 0.12, 0.14, 0.17, 0.21, 0.25$.
- But why this is the right thing to do?

Derivation of MaxEnt. Notation.

Start with $n$ independent trials, each with different $m$ outcomes.

Each sample is then just a string of length $n$:

\[ 1, m-1, m-2, 5, 6, 7, 3, 1, 2, 3, 5, 7\]

So sample space is $S^n = \{1, 2, \dots, m\}^n$ such that $|S^n| = m^n$.

Start with "ignorance knowledge" $I_0$ i.e.

\[ P(A | I_0) = \frac{M(n, A)}{|S^n|} \,,\]

where the multiplicity of $A$, $M(n, A)$, is just the number of distinct strings in $S^n$ such that $A$ is true.

Breaking down multiplicity $M(n, A)$ into a sum

Denote by $n_1, n_2, \dots n_m$ the number of times the trial came up with result $1, 2, \dots, m$ respectfully.

If the string is $1, 2, 1, 2, 2, 2, 3$, then $(n_1, n_2, n_3) = (2, 4, 1)$.

Suppose we have a restriction $R$ where $A(n_1, n_2, \dots, n_m)$ is true. If $A$ is linear in $n_j$ then

\[ M(n, A) = \sum_{n_j \in R} \frac{n!}{n_1!n_2!\dots n_m!} \]

Explicit example:

Rolling a die $20$ times. $A = \text{average roll is 4}$. Then pick $(n_1, n_2, n_3, n_4, n_5, n_6)$ so that $\sum n_i = 20$. If $\sum i * n_i = 4 * 20 = 80$, include the multinomial coefficient in the calculation of multiplicity of $A$:

\begin{align*} M(20, A) = \frac{20!}{1!1!1!12!4!1!} + \frac{20!}{1!1!1!13!2!2!} + \frac{20!}{1!1!2!10!5!1!} + \cdots \end{align*}

There are $283$ terms in the summation.

Deriving MaxEnt principle. Finally.

Let $W_{\max} = \max_{R} \frac{n!}{n_1! n_2! \dots n_m!}$. Then

\[ W_{\max} \leq M(n, A) \leq W_{\max} * \frac{(n + m - 1)!}{n! (m - 1)!} \]

Can be seen that $\text{\# of terms} \sim n^{m-1} / (n-1)!$, so

\[ \frac{1}{n} \log M(n, A) \to \frac{1}{n} \log (W_{\max}) \text{ as } n \to \infty\]

Introduce frequency distribution $f_j = n_j / n$. If $f_j$'s tend to constants as $n \to \infty$, use Stirling's approximation

\[ \frac{1}{n} \log M(n, A) \to H := - \sum_{j = 1}^{m} f_j \log f_j \,.\]

So the multiplicity can be found by determining the frequency distribution $\{ f_j \}$ which maximises entropy subject to $R$.

Convergence of Bayesian probabilities with Frequentists

We can further show that for $A = \sum_{i=1}^{m} g_i n_i$,

\[ P(\text{trial}_i = j | A, n, I_0) = \frac{M(n - 1, A - g_j)}{M(n, G)} = f_j \,. \]

(Trick) set $g_1 = \pi, g_2 = e$. If $A(n_2, n_2) = 3 \pi + 5 e$ is true, then $(n_1, n_2) = (3, 5)$. Can be shown that

\[ P(\text{trial}_i = j | \{n_j\}, n, I_0) = \frac{n_j}{n} \]

So even started with ignorant information $I_0$, we nevertheless produce the standard results.

So why does heat flow from hot objects to cold objects?

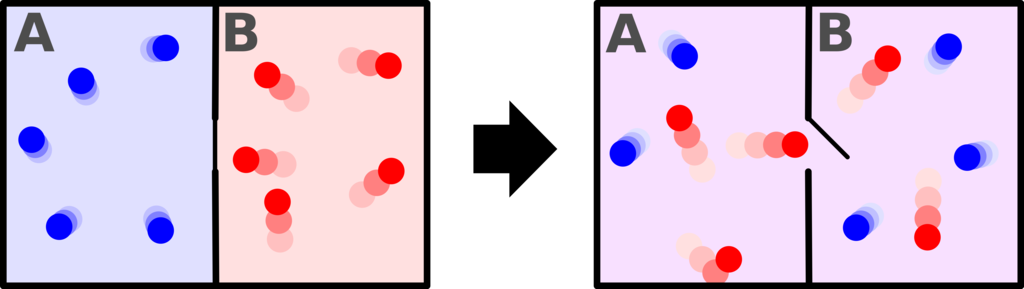
disorder increases

Enumerate energy states for each particle: $\{E_i^A\}, \{E_j^B\}$

No heat exchange. a) $\sum_{i \text{ odd}} P_i E_i = \bar{E}_A$ and b) $\sum_{i \text{ even}} P_{i} E_i = \bar{E}_B$ c) $\sum_{i \text{ odd}} P_i = \sum_{i \text{ even}} P_i = 1/2$.

With heat exchange. One restriction: d) $\sum_i P_{i} E_i = \bar{E}_A + \bar{E}_B$.

Restrictions a) & b) & c) $=>$ d) but $d)$ $\nRightarrow$ a) & b) & c). So entropy is bigger under just d).

Intro into Central Limit Theorem.

CLT

MaxEnt explains Central Limit Theorem.

Let $X_1, X_2, \dots, X_n$ be independent, identically distributed random variables. Then

\[ \frac{X_1 + X_2 + \dots + X_n - n \mu}{\sqrt{n}} \to \mathcal{N}(0, 1)\]

Why convergence? Why Gaussian?

Turns out: convolution: $X + Y$ is "forgetful", but keeps mean and variance fixed. And Gaussian is the MaxEnt-distribution with prescribed mean and variance.

The Wisdom of Crowds Revisited.

Ask everyone in China about the height of the Emperor.
1. Everyone's error is no more than $\pm 1$ meter.
2. There are $10^9$ inhabitants.
3. $1/\sqrt{10^9} \approx 3*10^{-5}$ accuracy by averaging everyone's guess?
What assumption of the CLT is broken?

Logical independence: $P(A|BC) = P(A|C)$, so knowledge that $B$ is true does not affect the probability we assign to A.
Causal independence: no physical cause.

Note: neither imply the other.

Advantages of Bayesian methods.

Bayesian methods unify statistical inference, probability theory, information theory under one mathematical framework.

"Information theory must precede probability theory and not be based on it." -- Kolmogorov

E.T. Jaynes derived procedures for multiple hypotheses testing, parameter estimation, significance testing and many more directly from the Cox's theorem.

Often times such derivations yield a new and deeper understanding of the statistical tools.

Some objections to the use of Bayesian framework addressed

Scientists shouldn't feed their prejudices into the result.

Counterargument 1: Probability is subjectively objective. Two Bayesians starting with the same state of information must arrive at the same conclusion. They are violating one of Cox's axioms otherwise.

Counterargument 2: Data can't speak for itself.

Whether data support the hypothesis depends on alternatives and prior information

There are 2 worlds:

World 1: there are two million birds, $100$ are crows, all black.
World 2: there are 2 million birds, $200,000$ are black crows, $1,800,000$ are white crows.

Then observing a black crow is evidence against the hypothesis that all crows are black.

Same data can be evidence against and for same hypothesis.

Applications in everyday thinking.

(Jaynes) Divergence views. 2 people exposed to a large number of same data don't have to agree.

(Jaynes) You can't prove yourself right in plausibility reasoning. You can only make predictions. If the predictions are correct - you learn nothing new!

Final remarks

Many of our applications lie outside the scope of conventional probability theory as currently taught. But we think that the results will speak for themselves, and that something like the theory expounded here will become the conventional probability theory of the future.

-- E.T. Jaynes. Probability: The Logic of Science

A scientist who has learned how to use probability theory directly as extended logic has a great advantage in power and versatility over one who has learned only a collection of unrelated ad hoc devices. As the complexity of our problems increases, so does this relative advantage. Therefore we think that, in the future, workers in all the quantitative sciences will be obliged, as a matter of practical necessity, to use probability theory in the manner expounded here.

-- E.T. Jaynes. Probability: The Logic of Science

Probability theory as an extension of logic

Motivation