Generating Ethereum address from scratch
In this blog post I would like to introduce readers into Elliptic Curve Cryptography and use this knowledge to construct an Ethereum address.
Part 1: Elliptic Curves
An Elliptic Curve is a curve define by the equation
\[y^2 = x^3 + ax +b,\]The curve has a number of nice properties, and one of them is that if take two points on the curve and draw a line through them, the line will intersect the curve at exactly one point. You can play around with this property using the Bokeh application below:
CODE
import numpy as np
from bokeh.layouts import column, row
from bokeh.models import CustomJS, Slider
from bokeh.plotting import ColumnDataSource, figure, show
def create_layout(a: int, b: int, start_xs=[1, 6], x_max=15, flip=False):
roots = np.roots([1, 0, a, b])
min_ = roots[np.isreal(roots)][0].real
while min_**3 + min_ * a + b < 0:
min_ += 0.0001
step = 0.01
x_vals = np.arange(min_, x_max, step)
y_vals = np.sqrt(x_vals**3 + a * x_vals + b)
start_xs = np.array(start_xs)
start_ys = np.sqrt(start_xs**3 + a * start_xs + b)
if flip:
start_ys[0] = -start_ys[0]
source = ColumnDataSource(data=dict(x=start_xs, y=start_ys))
line_xs = [x_vals.min()] + list(start_xs) + [x_vals.max()]
slope = (start_ys[1] - start_ys[0]) / (start_xs[1] - start_xs[0])
y_line_min = slope * (x_vals.min() - start_xs[0]) + start_ys[0]
y_line_max = slope * (x_vals.max() - start_xs[0]) + start_ys[0]
line_ys = [y_line_min] + list(start_ys) + [y_line_max]
source_line = ColumnDataSource(data=dict(x=line_xs, y=line_ys))
p1_slider = Slider(start=x_vals.min(), end=x_vals.max(), value=start_xs[0],
step=step, title="Point1")
p2_slider = Slider(start=x_vals.min(), end=x_vals.max(), value=start_xs[1],
step=step, title="Point2")
plot = figure(plot_width=400, plot_height=400)
plot.line(x_vals, y_vals, line_width=2)
plot.line(x_vals, -y_vals, line_width=2)
plot.circle('x', 'y', source=source, size=10, color="navy", alpha=0.5)
plot.line('x', 'y', source=source_line, line_width=1, color="black")
minus = "-" if flip else ""
callback = CustomJS(args=dict(source_dots=source,
source_line=source_line,
p1=p1_slider, p2=p2_slider),
code=f"""
const data = source_dots.data;
const x1 = p1.value;
const x2 = p2.value;
const x = data['x'];
const y = data['y'];
x[0] = x1;
x[1] = x2;
const y1 = {minus}Math.sqrt(Math.pow(x1, 3) + {a} * x1 + {b});
const y2 = Math.sqrt(Math.pow(x2, 3) + {a} * x2 + {b});
y[0] = y1;
y[1] = y2;
source_line.data['x'][1] = x1;
source_line.data['x'][2] = x2;
source_line.data['y'][1] = y1;
source_line.data['y'][2] = y2;
const slope = (y2 - y1) / (x2 - x1);
source_line.data['y'][0] = slope * (source_line.data['x'][0] - x1) + y1;
source_line.data['y'][3] = slope * (source_line.data['x'][3] - x1) + y1;
source_dots.change.emit();
source_line.change.emit();
""")
p1_slider.js_on_change('value', callback)
p2_slider.js_on_change('value', callback)
layout = column(
plot,
column(p1_slider, p2_slider),
)
return layout
l1 = create_layout(2, 29, flip=True)
l2 = create_layout(2, 29, flip=False)
show(row(l1, l2))
This property allows us to map 2 points on a curve to a 3 point, an operation that we will refer to as an addition (with respect to the curve). The reason we call this an addition, because it shares certain similarities with an arithmetic addition. However, we refine our addition to result in the reflected point, see illustration below:
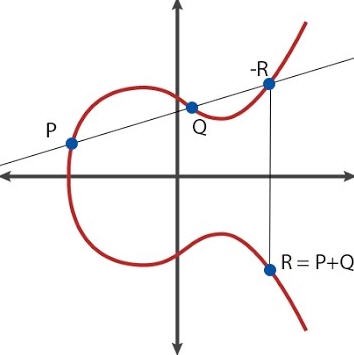
Algebraically, this means that
\[\begin{align} \begin{split} x_R &= s^2 - x_P - x_Q, \\ y_R &= y_P + s(x_R - x_P) . \end{split} \tag{1}\label{eqn:point_r} \end{align}\]where slope, \(s\), defined as
\[\frac{y_P - y_Q}{x_P - x_Q},\]when \(P \neq Q\), and
\[\frac{3x_P^2 + a}{2y_P},\]when \(P = Q\). Note that in this case the slope is just a tangent and is easy to derive:
\[\frac{\partial (y^2)}{\partial x} = \frac{\partial (x^3 + ax +b)}{\partial x} \implies \\ 2y \frac{\partial y}{\partial x} = 3x^2 + a.\]We can verify algebraically that \(y_R^2 = x_R^3 + ax_R + b\), meaning
\(R\) is on our curve. Finally, for our addition to be valid, we need to
define a point that would serve the role of \(0\). So, by definition,
\(P + O = P\), and \(-P + P = O\). My vague intuition is that I can think
of \(O\) as the entire x-axis.
Part 2: Mathematical Fields
If we pick a prime number \(p\), we can define multiplication, addition, subtraction and division module \(p\):
class Field:
def __init__(self, p: int):
self.p = p
def multiply(self, a: int, b: int) -> int:
return a * b % self.p
def add(self, a: int, b: int) -> int:
return (a + b) % self.p
def sub(self, a: int, b: int) -> int:
return (a - b) % self.p
def div(self, a: int, b: int) -> int:
b = b % self.p
if b == 0:
raise ZeroDivisionError
inv_b = egcd(b, self.p)[0] % self.p # Euclidean algorithm
return self.multiply(a, inv_b)Mathematically, this means that we have a field, \(\mathbb{F}_p\). Real numbers form a field too, so you probably have a good intuition for how fields work.
Here are arithmetic tables for \(\mathbb{F}_{7}\), skipping subtraction as I don’t have space:
|
|
|
Plot twist: we are now going to deal with an elliptic curve defined over \(\mathbb{F}_p\). Turns out the equations for addition with respect to a curve, \eqref{eqn:point_r}, are still well-defined: they only use simple arithmetic operations (*, /, +, -) anyway. Unfortunately, we no longer have the geometric intuition, as our curve plotted will now look like just a bunch of points.
Part 3: Toy Elliptic Curve over \(\mathbb{F}_{37}\)
I wrote some auxiliary code that implements fields and elliptic curves, attached in appendix. For now, let’s use play with it to get used to the elliptic curves over prime fields:
def generate_span(start_point): # keep adding until we hit zero
span = [start_point]
while not span[-1].zero:
span.append(span[-1] + start_point)
return span
ec = EC(11, 16) # initiate y^2 = x^3 + 11x + 16
field_37 = Field(37)
point1 = ec.point(field_37.n(0), None) # y=None will find a point on the curve
span1 = generate_span(point1)
> span1
[[0_₃₇, 4]_₁₁,₁₆,
[36_₃₇, 2]_₁₁,₁₆,
[5_₃₇, 23]_₁₁,₁₆,
[5_₃₇, 14]_₁₁,₁₆,
[36_₃₇, 35]_₁₁,₁₆,
[0_₃₇, 33]_₁₁,₁₆,
[None, None]_₁₁,₁₆] # zeroI started with a point \((0, 4)\), module 37, and kept adding it until I reached \(O\). I have to reach \(O\), because the number of points on the curve is finite, so they have to start repeating:
\[nP = mP \implies (n-m)P = 0,\]for some \(n \neq m\). Are there any more points on the curve? Let’s find out:
def find_outside_span(point):
span = generate_span(point)
for i in range(point.x.field.p):
try:
p = ec.point(point.x.field.n(i), None)
except ValueError:
continue
if p not in span:
return p
point2 = find_outside_span(point1)
>point2
[1_₃₇, 18]_₁₁,₁₆Yes, there’s at least one more point: \((1, 18)\). Any more?
> find_outside_span(point2)
NoneLooks like \((1, 18)\) generates all points on our curve. How many points do we have? 49:
> len(generate_span(point2)), len(span1)
49, 7In mathematics , we say that the order of point2 is 49, whilst the
order of point1 is 7, where order is the number of times we add until we
reach zero. point2 in this toy example plays the same role that number
\(1\) plays in integers: by adding \(1\) repeatedly we an generate all
positive integers. Same holds for point2: by adding it repeatedly we generate
all points on the curve. OK, hopefully you get a better feel for this object.
Let’s proceed.
Part 4: Ethereum Address
I went on vanity-eth.tk and generated a public and a private key:
0xeace72e038dd840a468986654448a7d6d3e1a750 # public
0xf6096531d756e52953455522cacc2a1effe504577233df66d3a3110231ff918c # privateWe have already covered all the material needed to replicate such computation. Both Ethereum and Bitcoin use an elliptic curve \(y^2 = x^3 + 7\) over \(\mathbb{F}_p\), where \(p = 2^{256} - 2^{32} - 2^{9} - 2^{8} - 2^{7} - 2^{6} - 2^{4} - 1\), a very large prime.
It turns out whilst calculating \(n * P = Q\), i.e. summing \(P\) with itself \(n\)-times, is computationally easy, finding \(n\), given \(P\) and \(Q\) is computationally hard. So the private key is \(n\), whilst the public key is \(n * P\), for some specified \(P\). Below is the code that defines the curve and the specified point, taken from the secp256k1 specs:
p = 2**256 - 2**32 - 2**9 - 2**8 - 2**7 - 2**6 - 2**4 - 1
# hex codes for compactness, those are just large integers
x = 0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
y = 0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8
point = EC(0, 7).point(Field(p).n(x), y)Finally, we can generate the public point using multiplication:
pp = 0xf6096531d756e52953455522cacc2a1effe504577233df66d3a3110231ff918c * pointThat’s almost our public key, but not quite. We now encode (x, y) coordinates of our public point in hex, to get something like
def public(self) -> str:
if self.x is None or self.y is None:
raise ValueError("Zero can't be public")
x = self.x.a if isinstance(self.x, Field.Int) else self.x
y = self.y.a if isinstance(self.y, Field.Int) else self.y
return f"{x:064x}{y:064x}"
> pp.public()
c662ecf3e1c45eefbacd6244863dff8a23e414fc7f52567dcaf1796c898730ab8392
c6811de16d4c235a7522b83cba9ed1824af40ac72932863689a342215033Finally, we compute Keccak-256 hash function on the public point, and take last 40 characters:
> pp.ethereum()
0xeace72e038dd840a468986654448a7d6d3e1a750Voilà!
Credits
Thanks to bellbind github account for his toy implementations and Timur Badretdinov for his blog post.
Appendix
ALL THE CODE
from __future__ import annotations
from typing import Optional, Union, Tuple
import math
import codecs
def to_subscript(n):
SUB = str.maketrans("0123456789", "₀₁₂₃₄₅₆₇₈₉")
return str(n).translate(SUB)
def egcd(a, b) -> Tuple[int, int, int]:
"""extended GCD
returns: (s, t, gcd) as a*s + b*t == gcd
>>> s, t, gcd = egcd(a, b)
>>> assert a % gcd == 0 and b % gcd == 0
>>> assert a * s + b * t == gcd
"""
s0, s1, t0, t1 = 1, 0, 0, 1
while b > 0:
q, r = divmod(a, b)
a, b = b, r
s0, s1, t0, t1 = s1, s0 - q * s1, t1, t0 - q * t1
return s0, t0, a
class Field:
class Int:
def to_int(self, other: Union[Field.Int, int]) -> int:
if isinstance(other, int):
return other
elif hasattr(other, 'a') and hasattr(other, 'field'):
assert self.field.p == other.field.p
return other.a
else:
raise NotImplementedError
def __init__(self, field: Field, a: int):
self.field, self.a = field, a
def __str__(self) -> str:
return str(self.a)
def __repr__(self) -> str:
return f"{self.a}_{to_subscript(self.field.p)}"
def __mul__(self, other: Union[Field.Int, int]) -> Field.Int:
return self.field.n(self.field.multiply(self.a, self.to_int(other)))
def __rmul__(self, other: int) -> Field.Int:
return self.__mul__(other)
def __add__(self, other: Union[Field.Int, int]) -> Field.Int:
return self.field.n(self.field.add(self.a, self.to_int(other)))
def __radd__(self, other: int) -> Field.Int:
return self.__add__(other)
def __sub__(self, other: Union[Field.Int, int]) -> Field.Int:
return self.field.n(self.field.sub(self.a, self.to_int(other)))
def __rsub__(self, other: int) -> Field.Int:
return self.field.n(self.field.sub(self.to_int(other), self.a))
def __neg__(self) -> Field.Int:
return self.field.n(self.field.sub(0, self.a))
def __truediv__(self, other: Union[Field.Int, int]) -> Field.Int:
return self.field.n(self.field.div(self.a, self.to_int(other)))
def __rtruediv__(self, other: int) -> Field.Int:
return self.field.n(self.field.div(self.to_int(other), self.a))
def __pow__(self, other: int) -> Field.Int:
return self.field.n(self.field.pow(self.a, other))
def __eq__(self, other: object):
if isinstance(other, (Field.Int, int)):
return self.field.eq(self.a, self.to_int(other))
return False
def __init__(self, p: int):
self.p = p
def n(self, a: int) -> Field.Int:
return Field.Int(self, a % self.p)
def multiply(self, a: int, b: int) -> int:
return a * b % self.p
def add(self, a: int, b: int) -> int:
return (a + b) % self.p
def sub(self, a: int, b: int) -> int:
return (a - b) % self.p
def div(self, a: int, b: int) -> int:
b = b % self.p
if b == 0:
raise ZeroDivisionError
inv_b = egcd(b, self.p)[0] % self.p
return self.multiply(a, inv_b)
def pow(self, a: int, n: int) -> int:
if n < 0:
return self.pow(self.div(1, a), -n)
r, m2 = 1, a
while n > 0:
if n & 1 == 1:
r = self.multiply(r, m2)
n, m2 = n >> 1, self.multiply(m2, m2)
return r
def eq(self, a: int, b: int) -> bool:
return (a - b) % self.p == 0
def sqrt(self, a: int) -> int:
a = a % self.p
for i in range(self.p):
if (i * i) % self.p == a:
return i
raise ValueError("not found")
class EC:
class Point:
def __init__(self, ec: EC,
x: Optional[Union[Field.Int, float]] = None,
y: Optional[Union[Field.Int, float]] = None):
self.zero = x is None and y is None
if x is not None and y is None:
y = ec.at(x)
self.ec, self.x, self.y = ec, x, y
def __eq__(self, other) -> bool:
return self.x == other.x and self.y == other.y
def __neg__(self) -> EC.Point:
if self.x is not None and self.y is not None:
return self.ec.point(self.x, -self.y)
return self.ec.point(x=None, y=None)
def __add__(self, other: EC.Point) -> EC.Point:
if self.x is None or self.y is None:
return other
if other.x is None or other.y is None:
return self
if self == -other:
return self.ec.point(None, None)
if self == other:
slope = (3 * (self.x)**2 + self.ec.a) / (2 * self.y)
else:
slope = (other.y - self.y) / (other.x - self.x)
x = slope**2 - self.x - other.x
y = slope * (self.x - x) - self.y
return self.ec.point(x, y)
def __mul__(self, n: int) -> EC.Point:
r, m2 = self.ec.point(None, None), self
# O(log2(n)) add
while n > 0:
if n & 1 == 1:
r += m2
n, m2 = n >> 1, m2 + m2
return r
def __rmul__(self, n: int) -> EC.Point:
return self.__mul__(n)
def __str__(self):
return f"[{self.x}, {self.y}]"
def __repr__(self):
t = to_subscript
return f"[{repr(self.x)}, {str(self.y)}]_{t(self.ec.a)},{t(self.ec.b)}"
def public(self) -> str:
if self.x is None or self.y is None:
raise ValueError("Zero can't be public")
x = self.x.a if isinstance(self.x, Field.Int) else self.x
y = self.y.a if isinstance(self.y, Field.Int) else self.y
return f"{x:064x}{y:064x}"
def ethereum(self) -> str:
# pip install pycryptodomex
from Cryptodome.Hash import keccak
public_key_bytes = codecs.decode(self.public(), 'hex')
keccak_hash = keccak.new(digest_bits=256)
keccak_hash.update(public_key_bytes)
keccak_digest = keccak_hash.hexdigest()
# Take the last 20 bytes
wallet_len = 40
wallet = '0x' + keccak_digest[-wallet_len:]
return wallet
def __init__(self, a: Union[Field.Int, float], b: Union[Field.Int, float]):
self.a, self.b = a, b # y^2 = (x^3 + ax + b) % p
def point(self, x: Optional[Union[Field.Int, float]], y: Optional[Union[Field.Int, float]]):
return EC.Point(self, x, y)
def y_squared(self, x: Union[Field.Int, float]) -> Union[Field.Int, float]:
return x**3 + self.a * x + self.b
def at(self, x: Union[Field.Int, float]) -> Union[Field.Int, float]:
if isinstance(x, (int, float)):
return math.sqrt(self.y_squared(x))
if isinstance(x, Field.Int):
return x.field.sqrt(self.y_squared(x.a))
raise NotImplementedError